Ecco un’interessante attività che ho impostato per la mia classe tenendo conto delle competenze pregresse, del percorso avviato quest’anno in geometria e della possibilità di proporre una sfida “particolare”. Questa attività è sicuramente trasversale perché, oltre a tener conto degli obiettivi da raggiungere in geometria, sfrutta e rende operative le competenze matematiche e si rifà anche al concetto di algoritmo come insieme di istruzioni organizzate in sequenza per il raggiungimento di un obiettivo. Per quanto concerne la geometria ho arricchito quanto affrontato lo scorso anno sulle caratteristiche dei poligoni (sulle quali stiamo lavorando nuovamente in questo periodo) e ripreso in mano il concetto di perimetro… oltre a sviluppare l’abilità nell’uso della squadra (misure e utilizzo preciso delle strumento per la creazione di figure geometriche); per quanto riguarda le competenze matematiche ho richiamato il concetto di misura e calcoli semplici con le misure di lunghezza, sfruttato le competenze acquisite nelle frazioni (richiamo del lavoro di terza ma soprattutto quello appena concluso quest’anno) e stimolato ragionamenti logici e deduttivi; con l’aiuto dell’algoritmo mi sono ricollagata alle attività che stiamo svolgendo in aula informatica nella piattaforma code.org con particolare riferimento all’artista del CorsoE in cui si parla di cicli di ripetizione.
L’attività in questione è la costruzione del Triangolo di Sierpiński. Il percorso si è sviluppato in due giornate da un’ora e mezzo l’una. Ovviamente ho cercato di sviluppare un percorso fattibile sia per la fascia d’età di riferimento ma anche per le competenze già acquisite. Ho deciso però di spingermi un po’ oltre, sfruttando l’occasione per stimolare nuove riflessioni. Il triangolo in questione è infatti un frattale. Troppo prematuro parlare di frattali in classe quarta ma non troppo presto per “fare amicizia” con un linguaggio matematico-scientifico che si porta dietro concetti “nuovi”. Proprio per questo motivo ho introdotto l’attività proponendo informazioni e curiosità per catturare l’attenzione e cercando di far capire, da subito, quale sarebbe stato il nostro campo di lavoro. Ho proiettato alla LIM direttamente dal mio iPad (dove ho creato la lezione su GoodNotes con la applepen) questa pagina:
Il richiamo alle attività svolte in informatica con il coding è palese. Emerge che il concetto di frattale è legato alla magia della natura che si esprime anch’essa in linguaggio matematico. Questo l’abbiamo già osservato quando abbiamo parlato della sequenza di Fibonacci (argomento che svilupperemo meglio il prossimo anno). Allo stesso tempo spunta fuori il blocco di ripetizione utilizzato nei nostri laboratori di coding che ci semplifica il lavoro quando dobbiamo ripetere la stessa istruzione più volte. Preciso che è possibile creare triangoli di Sierpinski con figure diverse ma noi ci concentreremo con la figura classica: il triangolo equilatero. Sarà più facile costruirlo ma ci consentirà anche di portare avanti una serie di ragionamenti su perimetro e fazioni.
Prima di tutto dobbiamo costruire il nostro triangolo equilatero. Richiamiamo alla mente ciò che sappiamo circa le caratteristiche di questo triangolo e per disegnarlo al meglio ci aiutiamo con un algoritmo. Il nostro lavoro sarà organizzato in questo modo: in una pagina scriveremo l’algoritmo pezzo per pezzo (non usando i blocchi visuali ma scrivendo le istruzioni in sequenza) e, accanto, nell’altra pagina “eseguiremo” le istruzioni… sino al completamento della consegna. I bambini operano sul quaderno con matita, squadra e penne di colori diversi mentre io utilizzo come quaderno la LIM quadrettata e gli strumenti in dotazione.
Alla LIM scrivo la prima istruzione e i bambini fanno lo stesso sul quaderno. Utilizzo la lettera maiuscola A rossa e chiedo ai bambini di eseguire l’istruzione “disegna un triangolo equilatero”. Riflettiamo insieme: essendo equilatero dovrà avere lati che misurano la stessa lunghezza. Organizziamo al meglio lo spazio del foglio e partiamo dalla base che dovrà essere lunga 16 cm (32 quadretti con quaderno a quadretti da 0,50 cm). Una volta tracciata la base troviamo il punto medio e, con la squadra e la matita, tracciamo l’altezza che si prolungherà sino alla parte alta del foglio senza tener conto della misura. A questo punto tracciamo il segmento (che dovrà misurare 16 cm) che unisce l’estremità destra della base all’altezza tracciata e facciamo lo stesso con l’altra estremità. In questo modo otteniamo un triangolo equilatero. Cancelliamo la parte eccedente dell’altezza, verifichiamo che tutti i lati del triangolo misurino 16 cm e, eventualmente correggiamo. Nominiamo il lato del nostro primo grande triangolo “lato o” o “lo” che misura 16 cm.
Passiamo a questo punto alla seconda istruzione B, che sarà anche quella di riferimento… perché dovrà essere ripetuta di volta in volta. “Bambini, per eseguire questa istruzione dobbiamo trovare i punti medi di ciascun lato. Qualcuno ricorda il concetto di punto medio?” Questo lavoro l’abbiamo fatto altre volte e ripassato il concetto di punto media quando abbiamo riparlato delle caratteristiche dei poligoni. I bambini comprendono che sarà necessario calcolare il punto medio dividendo per due la misura del lato, quindi 8 cm. Se il lato è il nostro intero… i due segmenti generati dall’inserimento del punto medio… saranno 1/2 dell’intero (quindi il nuovo lato più piccolo l1 =lo/2). A questo punto eseguiamo l’istruzione B unendo i punti medi tracciati e generando così tre nuovi triangoli uguali al triangolo-madre ma più piccoli della metà e un triangolo centrale capovolto. 
Verifichiamo (prendendo le misure) che tutti i triangoli siano equilateri con lati da 8 cm. l’uno.
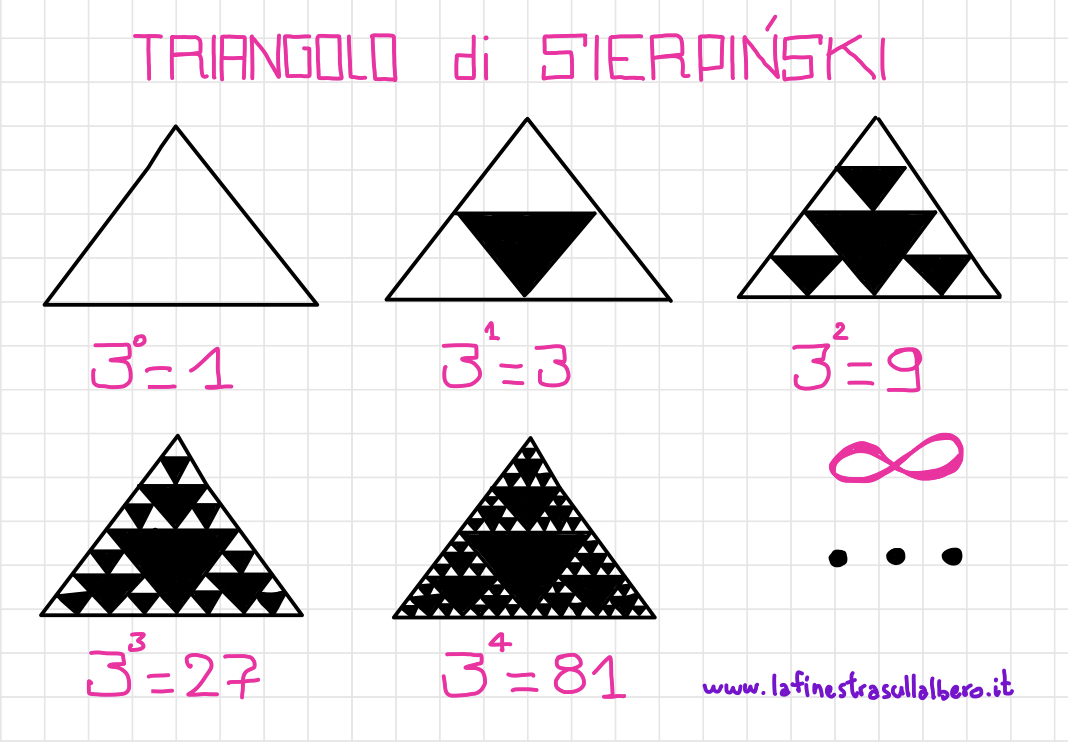
A questo punto passiamo all’istruzione C notando che si tratterà di ripetere quella B rimpicciolendo di volta in volta i triangoli ugualmente orientati rispetto al primo… ipoteticamente sino all’infinito. Questo, geometricamente parlando (quindi con la rappresentazione grafica) diventa impossibile per noi… ma matematicamente parlando si potrebbe tendere all’infinito perché qualsiasi misura potrebbe essere divisa per due. Ma senza farci venire i capogiri, mostro ai bambini lo schema che riprende le fasi che dovremmo raggiungere. Partiamo dal primo step con un triangolo, procediamo con il secondo step con 3 triangoli, al terzo con 9, al quarto con 27 e al quinto con 81. Per sapere quanti triangoli avremo di volta in volta stiamo semplicemente calcolando le potenze di 3. “Tre è il numero dei lati del triangolo e le potenze le vedremo il prossimo anno. Ma sappiate che sono la ripetizione della quantità iniziale, nel nostro caso 3, per se stesso un tot di numero di volte. Ad esempio 3 elevato 3 sarebbe 3x3x3 = 27! Ma questa è un’altra storia… e la vedremo meglio il prossimo anno. Per ora sappiate che esistono le potenze, che sono utili… e questo è un modo di utilizzarle e ragionarci su“. Procedo insieme a loro sino al terzo passaggio facendo notare che di volta in volta prenderemo in considerazione solo i triangoli orientati allo stesso modo del primo… quindi per non sbagliare consiglio di colorare in nero sempre quelli orientati diversamente e poi procedere misurando la metà dei lati dei triangoli bianchi ottenuti . Si lavora in silenzio, concentrati e con gran precisione. Non tutti riescono esattamente nell’intento ma la maggior parte sì. In una classe di 22 alunni: 5 ottengono triangoli perfetti e “puliti”; più della metà ottengono triangoli buoni (solo con qualche svista o con linee non proprio perfette); alcuni non riescono a ultimare il lavoro nei tempi stabiliti pur lavorando con precisione mentre qualcuno lavora di fretta e si perde o lavora in maniera imprecisa (ad esempio disegnando ad un certo punto triangoli isosceli). Io sono comunque molto soddisfatta soprattutto perché stanno imparando a lavorare in autonomia e ad auto-correggersi. Ecco il lavoro di una mia alunna (in rosso i punti medi individuati di volta in volta):
La settimana successiva riprendiamo in mano questa attività per riflettere sul concetto di perimetro. Dopo un veloce ripasso sul perimetro e qualche esercizio di calcolo del perimetro dei poligoni regolari, riflettiamo insieme a partire dai triangoli ottenuti con Sierpinski.
Anche in questo caso lavoriamo insieme passaggio dopo passaggio. Arriviamo alle conclusioni tramite ragionamenti e sfruttando quanto sappiamo. Io formulo domande chiave (perché so dove voglio andare a parare) e loro ipotizzano, rispondono e calcolano. Una volta stabiliti i punti in comune lavoriamo sul quaderno e alla LIM. Non tutti arrivano alle stesse conclusioni, alcuni intuitivamente riescono a dare contributi eccellenti, altri seguono il discorso e portano avanti dubbi utili, diversi preferiscono farsi trascinare dalla corrente e devo andarli a stanare nel loro rifugio sicuro. “Sappiate che lavoreremo insieme sino ad un certo punto… e poi vi lancerò una sfida. Chi segue i passaggi son certa che riuscirà a trovare la luce in fondo al tunnel 😉 ” 
Il lavoro che propongo non è semplice ma voglio che i miei alunni inizino a lavorare potendosi problemi. Terrò conto di chi sarà in grado di cogliere la sfida e mettersi in gioco. Non mi interessa sapere chi riuscirà da solo a risolvere la sfida (in classe mia solo una bambina, alla fine, vincerà la sfida alla perfezione) ma stimolare in loro la voglia di provarci e con criterio. Per questa attività, come per la precedente, l’attenzione e la concentrazione sono tutto! Si perdono i bambini che hanno difficoltà a mantenere attenzione e concentrazioni attivi. Questo è un buon esempio di lavoro utile a stimolare la capacità di ascolto dei contributi di tutti.
Ecco le fasi del lavoro svolto insieme:
1.Calcoliamo il perimetro del primo triangolo disegnato (Po) con lato 16 cm. –> 16 x 3 = 48 cm. Sin qui tutto bene.
2.Ragioniamo insieme per calcolare i perimetri totali di tutti i triangoli bianchi ottenuti nel secondo passaggio. Il nuovo lato è la metà del primo quindi misura 8 cm. Quanti lati ci sono ora in tutto? 3 triangoli quindi 9 lati… ossia 8 cm x 9 quindi P1= 72 cm. Se ragiono in termini frazionari (come si osserva nella figura sopra) ogni lato è un mezzo del precedente quindi 1/2 ripetuto 3 volte (ogni triangolo nuovo). 3lo è il perimetro iniziale ossia 48. Questo diviso la metà e poi moltiplicato per i nuovi triangoli. Stiamo calcolando i 3/2 del perimetro di partenza. E infatti 48:2 = 24, 24×3 = 72 cm. I conti tornano e il nostro ragionamento regge.
3.Cosa accade nel seguente passaggio? Osservo il lato grande: quanti punti medi osservo per lato? Ossia, per quanto è stato diviso lo? Quattro parti. E quanti triangoli più piccoli si sono ottenuti? Abbiamo 9 triangoli! Quindi calcolo 9/4 di 48 e ottengo 108 cm. Ma se ragiono in termini di misure e lati, posso anche dire che il lato da 16 cm diviso per 4 avrà triangoli da lati di 4 cm moltiplicati per il numero dei lati totali 27 (3 lati per 9 triangoli ) ossia un perimetro di 108 cm.
4.A questo punto lancio la sfida. Prova a calcolare il perimetro del passaggio seguente. Osserva sul quaderno il tuo triangolo, segui i passaggi e i ragionamenti fatti sino ad ora e concentrati su queste domande: Quanti triangoli bianchi vedi? In quante parti è stato frazionato lo?
Lavorano con grande concentrazione. E provano sino ad ottenere dei risultati. Non tutti riescono ma almeno ci provano, si mettono in gioco, e sono soddisfatta. Il nuovo perimetro è i 27/8 di 48 ossia 162 cm. Ogni nuovo lato misura infatti 2 cm che moltiplico per 81 (il numero dei lati (3 lati per 27 triangoli ottenuti) e ottengo un perimetro di 162 cm.
Ricollego questa attività anche al concetto di frazione impropria affrontato in matematica e osserviamo che il perimetro aumenta di volta in volta perché aumenta la quantità di triangoli a partire dal perimetro del primo triangolo iniziale. La matematica è davvero entusiasmante!
Per approfondire o sviluppare nuovi percorsi consiglio questo video davvero interessante. Forse rispolveriamo Sierpinski quando affronteremo l’area dei poligoni. Ma questa è un’altra storia!
